Chapter 5 Designing a reward function through symbolic judgments

In this chapter, we present the second contribution, which is the judging part from the conceptual architecture in Figure 3.2. First, Section 5.1 starts with an overview of this contribution, makes the link with the previous contribution, and motivates it with respect to the research question. We present two different models: the first, using logic rules, is described in Section 5.2, whereas the second, using argumentation, is described in Section 5.3. Section 5.4 details the experiments’ conditions, which are based on the previous chapter, and results are reported in Section 5.5. Finally, we discuss the two models’ advantages and limitations and compare their differences, in Section 5.6.

5.1 Overview

In the previous chapter, we defined and experimented the learning agent component of our architecture, to learn behaviours with ethical considerations. The logical next step is thus to guide the learning agents through a reward signal, which indicates the degree of their actions’ correctness, i.e., alignment with moral values. This corresponds to the judgment of behaviours in the global architecture presented in Section 3.3.

We recall that we do not know beforehand which action should an agent take, otherwise we would not need learning behaviours. This lack of knowledge stems from the environment’s complexity, and the question of long-term consequences. Would it be acceptable to take an action almost perfect, from a moral point of view, which leads to situations where it is difficult or infeasible to take further morally good actions? Or would it be better to take a morally good action, although not the best one, which leads to situations where the agent is able to take more good actions?

These questions are difficult to answer, without means to compute the weight of consequences, for each action in each situation. If the horizon of events is infinite, this is even computationally intractable.

However, we assume that we are able to judge whether a proposed action is a good one, based on a set of expected moral values. The more an action supports the moral values, the higher the reward. On the contrary, if an action defeats a moral value, its associated reward diminishes.

The task thus becomes: how to judge proposed actions and send an appropriate reward signal to agents, such that they are able to learn to undertake morally good actions? This is in line with our second research question: How to guide the learning of agents through the agentification of reward functions, based on several moral values to capture the diversity of stakes?

Traditionally, most reinforcement learning algorithms use some sort of mathematical functions to compute the rewards, as we did in the previous chapter. This seems rather intuitive, since the learning algorithm expects a real number, and thus reward functions usually output real numbers. However, such mathematical functions also entail disadvantages.

The first point is their difficulty to be understandable, especially to non-AI experts, such as external regulators, domain experts, lay users, … We argue that understanding the reward function, or the individual rewards that it produces, may help us understand the resulting agent’s behaviour. Indeed, the reward function serves as an incentive, it measures the distance with the behaviour that we expect from the agent, and thus intuitively describes this expected behaviour.

A second point is that some processes are easier to describe using symbolic reasoning rather than mathematical formulas. As we have seen in the state of the art, many works in Machine Ethics have proposed to use various forms of symbolic AI, such as argumentation, logic, event calculus, etc. Symbolic reasoning has already been used to judge the behaviour of other agents’, and we propose to extend this judgment to the computation of rewards.

Symbolic formalizations allow to explicitly state the moral values, their associated rules, and the conflicts between rules. In this chapter, we propose to apply two different symbolic methods to design judgment-based reward functions. First, we partially use the Ethicaa platform (Cointe et al., 2016) to create judging agents based on logic reasoning, beliefs, and Prolog-like rules. The second alternative uses argumentation graphs, with arguments and attack relations between them, to compute the judgment.

Figure 5.1 shows the abstract architecture of this idea, without taking into account the details of either logic-based or argumentation implementations. On the right-side of the figure, learning agents still receive observations from the environment, and they output actions to the environment. However, we can see that the “Compute reward” function, which was previously within the environment, is now “agentified”, by introducing judging agents, on the left side of the figure. To perform this computation, judging agents receive the observations from the environment, and actions from learning agents (through the environment).

We want our learning agents to receive rewards based on multiple moral values, as highlighted by our objective O1.1. Each judging agent is attributed to a unique moral value, and rely on this explicitly defined value and its associated moral rules to determine the reward that should be sent to each learning agent, as part of their judgment process. It ensues that multiple rewards are produced for each learning agent. However, the learning algorithm expects a single, scalar reward. Thus, rewards from the different judging agents are aggregated before they are sent to learning agents.

Figure 5.1: Architecture of the symbolic judgment. The environment and learning agents are the same as in the previous chapter, but the rewards’ computation is moved from the environment to newly introduced judging agents, which rely on explicitly defined moral values and rules.

The two propositions, logic-based and argumentation-based judging agents, are detailed below, as well as several experiments that demonstrate learning agents are able to correctly learn from such symbolic-based rewards. We then discuss the differences between these 2 propositions, advantages and drawbacks with respect to the numeric-based reward functions, and remaining limitations and perspectives.

Remark. These two implementations outcome from collaboration with interns. Jérémy Duval worked on the implementation of the first method, based on Ethicaa agents (Duval, 2020 ; Chaput, Duval, Boissier, Guillermin, & Hassas, 2021). Benoît Alcaraz worked on the second method, judging through argumentation (Alcaraz, 2021). Christopher Leturc, who was at the time an associate lecturer at École des Mines St-Étienne (EMSE), brought his expertise on argumentation for this second internship.

5.2 Designing a reward function through logic rules

In this section, we first explain the motivations for combining a symbolic judgment with reinforcement learning agents, and for using logic-based agents to do so. To perform the symbolic judgment, we then introduce new, specific judging agents that are based on Ethicaa agents. Finally, the proposed model for the computation of rewards, which can be integrated with a reinforcement learning algorithm, is presented.

5.2.1 Motivations

As mentioned previously, this contribution focuses on leveraging simplified Ethicaa agents (Cointe et al., 2016) to judge the learning agents’ actions, and determine an appropriate reward. There are multiple advantages and reasons behind this idea.

• The combination of symbolic (top-down) judgments and neural (bottom-up) learning constitutes a hybrid approach, which cumulates advantages of both.
  • Neural learning has the ability to generalize over unexpected situations.
  • Symbolic reasoning offers a better intelligibility of the expected behaviour, and the possibility to integrate prior knowledge from domain experts.
• Agentifying the reward function, by introducing judging agents, allows the judging and learning agents to evolve independently, and paves the way to co-construction.
  • Judging agents’ rules can be updated by human designers, and learning agents must adapt their behaviour to comply with the judgments resulting from the new rule set. This opens to a perspective of human-centered AI with a human-in-the-loop schema.
• As mentioned in our general framework, intelligibility is important, especially to confirm whether the expected behaviour is aligned with our desired moral values.
  • The judgment process is implemented on explicit moral values and rules, expressed in a symbolic form, which improves the intelligibility.
• We obtain a richer feedback by combining the judgment of multiple judging agents, each corresponding to a single moral value.
  • This facilitates the implementation of the judgment process on one single moral value, and makes it more intelligible.
  • It also offers the possibility of more complex interactions between different judging agents each in charge of a single moral value with a dedicated rule set, such as negotiation processes.
  • Finally, it offers a way to update rules by adding, removing, or replacing judging agents.

We begin by introducing our judging agents, which are based on Ethicaa agents, how they work, and how they produce rewards.

5.2.2 Judging agents

To perform symbolic judgments with respect to given moral values and rules, we leverage the existing Ethicca agents (Cointe et al., 2016) that we have already mentioned in the State of the Art. These agents use the Beliefs - Desires - Intentions (BDI) architecture, and have an ethical judgment process to determine which actions are acceptable in a given situation.

An Ethicaa agent may perform a judgment on itself to determine which action it should take, or on another agent to determine whether it agrees with the other agent’s behaviour. We propose to adapt this judgment of others to compute the reward functions for learning agents. The original Ethicaa agent includes several processes, such as the awareness and evaluation processes, to obtain beliefs about the situation, and determine the feasibility on an action. We ignore such processes, as we judge actions already taken, and focus on the “goodness process”, retaining only the components that we need for our approach. Figure 5.2 represents such a simplified agent, with an explicit base of moral rules (MR), and moral values in the form of “value support” rules (VS).

Figure 5.2: The Goodness Process of Ethicaa agents, adapted from Cointe et al. (2016).

Our proposed simplified agents use their beliefs about the current situation (\(\Beliefs\)), the moral values (VS), the moral rules (MR), and the knowledge about actions (A) to produce a Moral Evaluation (\(\ME\)) of the actions. The Moral Evaluation returns a symbol, either \(\moral\), \(\immoral\) or \(\neutral\), from which we will compute the reward. We describe how we leverage this for our proposed model in the next section.

5.2.3 The proposed model: LAJIMA

We now describe the Logic-based Agents for JudgIng Morally-embedded Actions (LAJIMA) model, which is represented in Figure 5.3. Each judging agent contains an explicit moral value (VS) and associated moral rules (MR). They receive observations (\(\mathbf{o_l}\)) that are transformed into beliefs (\(\Beliefs\)), and actions (\(\mathbf{a_l}\)) that are similarly transformed into symbols (\(\mathcal{A}\)). Their judgment process relies on a moral evaluation function (\(\ME\)) for each of the actions component \(a_{l,1}, a_{l,2}, \cdots, a_{l,d}\). The moral evaluation function leverages the moral value (VS) and moral rules (MR) to do so. Symbolic moral evaluations compose the judgment of each judging agent \(j\), which is later transformed into a numeric feedback through the \(\Feedback\) function. Per-judge feedbacks are finally aggregated to form the reward \(r_l\) sent to the learning agent \(l\).

Figure 5.3: The judgment process of logic-based judging agents, which produces a reward as a scalar value for a learning agent \(l\). This process is duplicated for each learning agent. The symbolic judgments are then transformed as numbers through the feedback function \(\Feedback\), and finally averaged to form a scalar reward \(r_l\).

This contribution focuses on the reward function, and, for all things necessary, we assume the same DecPOMDP framework as described in the previous chapter. More specifically, the reward functions we will construct through judging agents work with any RL algorithm, under two assumptions:

• Observations and actions are multi-dimensional and continuous.
• RL agents expect a scalar reward signal.

These assumptions are sufficiently generic to support a large part of existing RL algorithms, in addition to our own Q-SOM and Q-DSOM algorithms. They mean that judging agents will have to handle real vectors as inputs, and produce a real scalar as output.

At each step \(t+1\) of the simulation, after learning agents took an action at step \(t\), observations and executed actions are sent to judging agents. We recall, from the DecPOMDP framework 4.1, that an observation \(\mathbf{o_{l,t}}\) is a vector \(\in \ObsSpace_l \subseteq \RR^g\), and an action \(\mathbf{a_{l,t}}\) is a vector \(\in \ActionSpace_l \subseteq \RR^d\). In this case, observations received by judging agents are the same as observations received by learning agents, yet they do not know the full state of the environment, nor the exact process that learning agents used. In Ethicaa’s vocabulary, this is deemed to be a partially informed ethical judgment, since judging agents have some but not all information about the judged agents.

From these observations, judging agents generate beliefs (\(\Beliefs\)) about the current situation, simply by creating a belief for each component of the observation vector \(\mathbf{o_l}\), with the same name as the component, and a parameter that corresponds to the component’s value. This produces symbols that can be handled by the judging agents’ moral evaluation mechanism, from the numeric vectors.

Example 5.1 Let us imagine a learning agent \(l\) that receives an observation vector \(\mathbf{o_l}\) \(= \left[ 0.27, 0.23, 0.35, 0.29, 0.51, 0.78, 0.47, 0.64, 0.95, 0.65 \right]\). A judging agent will thus generate the following beliefs when judging \(l\): \(\texttt{storage(0.27)}\), \(\texttt{comfort(0.23)}\), \(\texttt{payoff(0.35)}\), \(\texttt{hour(0.29)}\), etc.

Similarly, judging agents must judge actions based on symbols, whereas enacted actions by learning agents are vectors. Actions imply an additional difficulty, compared to observations: a single action vector represents in fact several “sub-actions” that happen at the same time, on different dimensions, e.g., consuming energy from the grid, and buying energy from the national network. A judging agent may judge one of the dimensions as supporting its associated moral value, whereas another dimension defeats the same moral value. Since they must return a scalar reward from their judgment, what should the judging agent return in this case?

To simplify this, we propose to decompose the enacted action into a set of action symbols \(\left\{ \forall i \in [[1,d]] : \mathbf{a}_{l,i} \right\}\), where \(l\) is the learning agent, \(\mathbf{a_l}\) is the enacted action by \(l\), i.e., a vector of \(d\) components, and \(\mathbf{a}_{l,i}\) is the \(i\)-th component, i.e., a real value. Each “action symbol” will be first judged individually, before being aggregated by the judging agent. As for the observations, a belief is generated with the component name and the component value as a parameter, for each component. However, contrary to the observations, the actions are scaled accordingly to the learning agent’s profile.

Example 5.2 Let us imagine a learning agent with a “Household” building profile, which has an action range of \(2,500\)Wh. The agent chooses an action vector \(\mathbf{a_l} =\) \(\left[ 0.78, 0.80, 0.53, 0.36, 0.52, 0.95 \right]\). As a result, the action truly enacted by the agent is the action vector, scaled by the action range, i.e., \(\left[ 0.78 \times 2500, 0.80 \times 2500, \cdots \right]\). The judging agent will therefore generate the following beliefs: \(\texttt{consumegrid(1950)}\), \(\texttt{store(2000)}\), etc.

Judging agents use the set of generated scalar values, known moral values and associated moral rules to determine if each component of the action, or “action symbol” supports or defeats their moral value. Moral rules are logical predicates expressing the support (or defeat) of an action component to a moral value, based on observations. To do so, we define the Moral Evaluation mechanism of judging agent \(j\) as a function \(\ME_j : \BeliefSpace \times \RR \rightarrow \ValSpace\), where we define \(\BeliefSpace\) as the space of possible beliefs about the situation, and \(\ValSpace\) as the set of possible valuations \(\ValSpace = \left\{ \moral, \immoral, \neutral \right\}\).

For example, the following lines, which are in a Prolog-like language, indicate that a learning agent’s action supports the sub-value of “promoting grid autonomy” if the quantity X associated to the buy_energy component is not more than \(100\)W. This sub-value is related to the environmental sustainability value, and each action component is judged individually and receives a moral evaluation, with respect to this moral value. If the action component defeats the moral value, or one of its sub-values, the evaluation is said to be \(\immoral\). Otherwise, if the action component supports the value, its evaluation is said to be \(\moral\). A default \(\neutral\) evaluation is assigned when the action component neither supports nor defeats the value.

valueSupport(buy_energy(X), "promote_grid_autonomy") :- X <= 100.
valueDefeat(buy_energy(X), "promote_grid_autonomy") :- X > 100.

subvalue("promote_grid_autonomy","env_sustain").

moral_eval(_,X,V1,immoral):- valueDefeat(X,V1) & subvalue(V1,"env_sustain").
moral_eval(_,X,V1,moral):- valueSupport(X,V1) & subvalue(V1,"env_sustain").
moral_eval(_,_,_,neutral).

Remark. Note that, in the previous example, the subvalue fact highlights the possibility of creating a value hierarchy, represented by the “VS” knowledge base of value supports. In our case, this hierarchy is not necessary and can be simplified: we use it mainly to make the code more understandable, by aptly naming the sub-values, e.g., here promote_grid_autonomy for actions that avoid buying too much energy from the national grid.

The judgment of a learning agent \(l\) by a judging agent \(j\) is thus the Moral Evaluation on every action symbol. Mathematically, we define \(\Judgment_j(l) = \left\{ \forall i \in [[1,d]] : \ME_j(\texttt{beliefs}(\mathbf{o_l}), a_{l,i}) \right\}\), where \(\mathbf{o_l}\) is the observation vector received by \(l\), and \(\mathbf{a_l}\) is the action vector chosen by \(l\).

A judging agent represents a single moral value; however, we want to judge a learning agent’s behaviour based on various moral values. A learning agent \(l\) is judged by all judging agents, which results in a list of lists of valuations.

Example 5.3 Let \(d=3\) the size of an action vector, \(l\) be a learning agent, and \(j_1, j_2\) two judging agents. To simplify the notation, we have \(\mathbf{B} = \texttt{beliefs}(\mathbf{o_l})\). Assume the judgments received by \(l\) is \[\begin{align*} & \left\{ \Judgment_{j_1}(l), \Judgment_{j_2}(l) \right \} \\ &= \left\{ \left\{ \texttt{ME}_{j_1}(\mathbf{B}, a_{l,1}), \texttt{ME}_{j_1}(\mathbf{B}, a_{l,2}), \texttt{ME}_{j_1}(\mathbf{B}, a_{l,3}) \right\}, \left\{ \texttt{ME}_{j_2}(\mathbf{B}, a_{l,1}), \texttt{ME}_{j_2}(\mathbf{B}, a_{l,2}), \texttt{ME}_{j_2}(\mathbf{B}, a_{l,3}) \right\} \right\} \\ &= \left\{ \left\{ moral, neutral, neutral \right\}, \left\{ immoral, immoral, moral \right \} \right\} \end{align*}\]

In this example, we can see the first judging agent \(j_1\) deemed the first dimension of the action \(a_{l,1}\) to be moral, i.e., consistent with its moral value and rules, whereas the second judging agent \(j_2\) deemed this same dimension to be immoral, i.e., inconsistent with its moral value and rules. The second dimension of the action \(a_{l,2}\) was deemed neutral by the first judge, and immoral by the second judge; the third and final dimension \(a_{l,3}\) was deemed neutral by the first judge, and moral by the second.

The reward function \(\RewardFn_l : \StateSpace \times \ActionSpace_l \times \StateSpace \rightarrow \RR\) must return a single, real number \(r_l\). However, we have a list of lists of valuations. Additionally, as we saw in the previous example, we may have conflicts between judgments, both within a single judge, and between judges. A judge may determine that some components of the action are immoral and others moral; multiple judges may determine that the same component of an action is both immoral and moral, according to their own different moral values.

We propose the following method to transform the set of valuations, although many other methods are possible. Such methods, how they differ with ours, and what these differences imply, are discussed in Section 5.6.

The Feedback function \(\Feedback : \left( \ValSpace^d \right)^{\length{\JAgts}} \rightarrow \RR^{\length{\JAgts}}\) transforms the valuations into a list of numbers. The judgment of each judging agent, i.e., a list of valuations, is transformed into a single number, by counting the number of \(\moral\), and dividing it by the sum of the number of \(\moral\) and \(\immoral\) valuations. This means that the more \(\moral\) valuations an action receives, the more it will tend towards \(1\). On the contrary, the more \(\immoral\) valuations an action receives, the more it will tend towards \(0\). If an action only received \(\neutral\) valuations, we consider it was neither good nor bad, and we set the number to \(0.5\) as a special case. We can note that this special case also corresponds to a situation where an action received as much \(\moral\) valuations as \(\immoral\).

We thus have a single number for each judging agent, which resolves conflicts within judges. Then, to solve the conflicts between judges, and produce a single reward for all judges, we set the reward \(r_l\) to be the average of these judgment numbers produced by each judging agent.

Example 5.4 We reuse the same judgments from example 5.3: \(\Judgment_{j_1}(l) =\) \(\left\{ moral, neutral, neutral \right\}\), and \(\Judgment_{j_2}(l) = \left\{ immoral, immoral, moral \right \}\). The first judgment contains \(1\) moral valuation, and \(0\) immoral; thus, the resulting number is \(\frac{1}{1+0} = 1\). On the other hand, the second judgment contains \(1\) moral valuation but \(2\) immoral valuations; thus, its resulting number is \(\frac{1}{1+2} = \frac{1}{3}\). In other words, \(\mathbf{f_l} =\) \(\Feedback\left( \left\{ \left\{ moral, neutral, neutral \right\}, \left\{ immoral, immoral, moral \right\} \right\} \right) =\) \(\left\{ 1, \frac{1}{3} \right\}\). Finally, the reward produced by the aggregation of these two judgments is simply the average of these numbers, i.e., \(r_l = \texttt{average}(\mathbf{f_l}) = \texttt{average}(\left\{ 1, \frac{1}{3} \right\}) = \frac{2}{3}\).

Algorithm 5.4 summarizes the judgment process that we defined in this section.

Figure 5.4: Logic-based judgment process algorithm

The foreach loop that begins on line 3 performs the judgment of all learning agents individually and sequentially. Each judging agent computes its beliefs over the observations \(\mathbf{o_l}\) received by a learning agent \(l\) (line 5), and uses them to judge each component of the action parameters (lines 7-9). The judgment for each dimension of the action is retained in a vector, so that the judge can later count the number of \(\texttt{moral}\) and \(\texttt{immoral}\) valuations (lines 14-16). Remember that, if the learning agent received only \(\texttt{neutral}\) valuations by a given judge, a default reward of \(\frac{1}{2}\) is attributed (lines 13 and 19). Finally, the reward ultimately received by a learning agent is the average of the per-judge rewards (line 22).

5.3 Designing a reward function through argumentation

We now propose a second method to design the reward function as symbolic judgments, through argumentation. The differences between logic rules and argumentation, their respective advantages and drawbacks, are discussed in Section 5.6.

5.3.1 Motivations

• Argumentation graphs offer a rich structure, by relying on the notion of arguments and attack relations. This allows explicit conflicts, represented by attacks between arguments, and offers a finer control over the targeted behaviour. In particular, it is easier to reprehend an undesired behaviour, by attacking arguments when specific conditions are met. For example, let us imagine that an agent learned to hoard energy at a time step \(t\) in order to give energy at a time step \(t+1\), therefore receiving praises for its “generous” behaviour at \(t+1\). If the hoarding behaviour at \(t\) is problematic, we may add an argument to the graph, which is activated when the agent stored a lot of energy at the previous step, and which attacks the pro-argument of having given energy. Thus, this pro-argument will be killed in such situations, which will prevent the agent from receiving a high reward: it will have to stop its hoarding behaviour to get better rewards.

• Note that it is easier for designers to structure the moral rules through the graph, as mentioned in the previous point. The attack relationship makes explicit the impact of an argument on another.

• Additionally, argumentation using a graph structure makes it feasible to visualize the judgment process, by plotting the arguments as nodes and attacks as edges between nodes. Non-developers, such as external regulators, lawyers, ethicists, or even lay users, can look at the graph and get a glimpse of the judgment function.

• Arguments themselves, and whether they were activated at a given time step \(t\), can be leveraged to understand the learnt and exhibited behaviour. For example, if the argument “has given energy” was activated, we can understand why the agent received a high reward. Or, on the contrary, if both arguments “has given energy” and “has previously hoarded energy” were activated, we can understand why the agent did not receive a high reward, although its actions at this specific time step seemed praiseworthy. They can be further used in explanations techniques: whereas we do not consider our method an explanation technique per se, these arguments represent elements of explanations that can be leveraged in explanation methods to explore and understand the expected behaviour, the incentives that led to each reward and ultimately that led to learn a given behaviour, and compare the exhibited behaviour to the expected one. In most AI techniques, these elements simply do not exist.

• Finally, the previous points may help us diminish the reward hacking risk, i.e., the possibility that an agent learns to optimize the reward function through an undesired (and unexpected) behaviour. A classic example is an agent that is rewarded based on the distance towards a goal, and which may find that it is more profitable to indefinitely circle as close as possible to the goal, in order to obtain an infinitely positive reward. Such reward hacking can, first, be detected by looking at the sequence of activated arguments. Without using argumentation, we might detect that something is off, by seeing a sequence of low then high rewards, e.g., \(0.2, 0.8, 0.2, 0.8\), but we might not understand what or why. We again take the example of the “hoarding then giving” behaviour presented earlier. Looking at arguments’ activations might reveal that, when the reward is low, the argument “agent stored too much energy” was activated; when the reward is high, the argument “agent gave a lot of energy” was activated. We can thus understand what the problem is. Secondly, the reward hacking can be fixed, by adding new arguments that prevent such hacking, as we have already mentioned.

5.3.2 Argumentation

Before introducing our AJAR model in the next section, based on argumentation decision frameworks, we briefly cover some necessary knowledge about argumentation.

Abstract argumentation frameworks, first introduced by Dung (1995), allow us to express knowledge as a set of arguments, such as “There are clouds today”, “The weather is nice”. Arguments are arranged as nodes of a directed graph, where the links, or edges, between nodes represent binary attack relations. For example, the argument “There are clouds today” attacks “The weather is nice”. This means that, if we consider the argument “There are clouds today” as true, or alive, in the current situation, it will be difficult to accept the argument “The weather is nice” as well. An example is given in Figure 5.5.

Figure 5.5: Simple example of an argumentation graph that contains 5 arguments (a, b, c, d, and e), represented by nodes, and 6 attack relations, represented by edges. Argument a attacks b, b attacks a and c, c attacks e, d attacks c, and e attacks a.

Multiple argumentation frameworks exist, e.g., attacks can be weighted (Coste-Marquis, Konieczny, Marquis, & Ouali, 2012), bipolar frameworks bring the notion of supporting an argument in addition of attacking (Amgoud, Cayrol, Lagasquie-Schiex, & Livet, 2008), arguments and attacks can have a probability (Li, Oren, & Norman, 2011), etc. In this contribution, we want to leverage the argumentation to produce a judgment of an agent’s behaviour. This can be seen as some sort of decision, where the possible outcomes are “The agent’s action was moral in regard to this specific moral value”, or “The agent’s action was immoral in regard to this specific moral value.”

We propose to use a simplified version of the Argumentation Framework for Decision-Making (AFDM) of Amgoud & Prade (2009). Their model considers that multiple decisions can be possible, whereas in our case, we only need to determine the degree to which an action can be considered moral, or immoral. We thus restrict our arguments to be pros, cons, or neutral arguments, and drop the set of decisions. This simplified version, instead of targeting decision-making, focuses on judging decisions, and we thus name it Argumentation Framework for Judging a Decision (AFJD).

Definition 5.1 (AFJD) An Argumentation Framework for Judging a Decision (AFJD) is defined as a tuple:

\(AF = \left\langle \Args, \Att, \Fp, \Fc \right\rangle\), where:

• \(\Args\) is a non-empty set of arguments. An argument is represented by a name, and has an aliveness condition function. This function is defined as \(\texttt{alive} : \StateSpace \rightarrow \mathbb{B}\), where \(\StateSpace\) is the space of world states, and \(\mathbb{B} = \left\{0, 1\right\}\) is the set of boolean values. It determines whether the argument can be considered “true” in the current state of the world, or “false”, in which case the argument is ignored.
• \(\Att\) is a binary relation named the attack relation, defined on pairs of arguments, such that \(A \mathbin{\Att} B\) means that argument \(A\) attacks argument \(B\).
• \(\Fp \in 2^{\Args}\) (for pros) is the set of pro-arguments, which indicate that the currently judged action was a moral one.
• \(\Fc \in 2^{\Args}\) (for cons) is the set of con-arguments, which indicate that the currently judged action was an immoral one.

To simplify notations in the sequel, we will refer to the elements of an AFJD through subscripts. In other words, for a given \(AF = \left\langle \Args, \Att, \Fp, \Fc \right\rangle\), we will note: \(AF_{[\Args]}=\Args\), \(AF_{[\Att]}=\Att\), \(AF_{[\Fp]}=\Fp\), \(AF_{[\Fc]}=\Fc\).

We will have to filter out arguments that cannot be considered as alive in the current situation, before we can make a decision. For example, if in the current situation, there are no clouds, then we disable the “There are clouds today”. Disabling an argument removes the node from the graph, as well as its attacks on other arguments of the graph. Formally, we call this filtered graph a “sub-AFJD”, i.e., an AFJD which is some subset of another AFJD: its arguments are a subset of the other AFJD’s arguments, and, by extension, its attack relation, pros, and cons are also subsets. We thus define the set of all possible sub-AFJD as:

\[\begin{align*} \mathcal{P}(AF) := \{ \left\langle \Args',\Att', \Fp', \Fc' \right\rangle : \quad & \Args' \subseteq AF_{[\Args]}, & \\ & \Att' \subseteq \Args'^{2} \cap AF_{[\Att]}, & \\ & \Fp' \subseteq \Args' \cap AF_{[\Fp]}, & \\ & \Fc' \subseteq \Args' \cap AF_{[\Fc]} & \} \end{align*}\]

As arguments may attack each other, and we want to compute the compliance of the learning agent’s action, we need a way to determine whether we should take a specific argument into account.

Example 5.5 (Attacking and defending arguments) Let us consider an argumentation graph composed of 3 arguments. The first one, \(arg_1\), says “The agent did not consume too much”. A second one, \(arg_2\) attacks \(arg_1\) and says “The agent consumed more than the average of all agents”. Finally, a third argument \(arg_3\) attacks \(arg_2\): “The agent had been in short supply for several time steps”. As \(arg_2\) attacks \(arg_1\) and \(arg_3\) attacks \(arg_2\), we say that \(arg_3\) defends \(arg_1\). Which arguments should be taken into account to judge the agent’s action? As \(arg_2\) attacks \(arg_1\), we might be tempted to ignore \(arg_1\), however, \(arg_3\) also attacks \(arg_2\). Thus, if we ignore \(arg_2\), can we keep \(arg_1\) as well?

In argumentation theory, this problem is known as defining acceptability. An argument that is inacceptable should not be taken into account by the judge, contrary to an acceptable argument. Acceptability is often based on the notion of conflictness between arguments. The following definitions, conflict-freeness and acceptability, are paraphrased from Dung (1995, p. 6).

Definition 5.2 (Conflict-freeness) Let \(\Args\) be a set of arguments, and \(\Att\) be an attack relationship on \(\Args\). A subset of arguments \(\SA \subseteq \Args\) is said to be conflict-free, with respect to \(\Att\), if and only if \(\not\exists \left(A,B\right) \in \SA\) such that \(A \mathbin{\Att} B\).

Definition 5.3 (Acceptability) Let \(\Args\) be a set of arguments, \(\Att\) be an attack relationship on \(\Args\), and \(\SA\) be a subset of arguments, such that \(\SA \subseteq \Args\). For each argument \(A \in \Args\), \(A\) is said to be acceptable with respect to \(\SA\), if and only if \(\forall B \in \Args : B \mathbin{\Att} A, \exists C \in \SA, C \mathbin{\Att} B\). In other words, an argument is acceptable with respect to a set, if all arguments that attack it are themselves attacked by at least an argument in the set. This represents some sort of “defense” between arguments: an argument \(A\) is defended by \(C\), if \(B\) attacks \(A\) and \(C\) attacks \(B\). The “defense” can be extended to the subset \(\SA\): if the arguments in \(\SA\) defend \(A\) by attacking all its attackers, then we say that \(\SA\) defends \(A\).

We can note from these two definitions that acceptability depends on the considered set. It is possible to find a conflict-free set, in which all arguments are acceptable, but maybe another set exists, holding the same properties. In this case, which one should we choose? And more importantly, why?

To solve this question, argumentation scholars have proposed various definitions of admissible sets of arguments, called extensions. The simplest one may be the admissible extension, while others propose the complete extension, stable extension, or preferred extension (Dung, 1995). We define a few extensions that we will use in our proposed algorithm; they are paraphrased from Caminada (2007, see Definition 3, p.2) to be slightly more explained.

Definition 5.4 (Extensions) Let us consider \(\Args\) a set of arguments within an Argumentation Framework, and \(\SA \subseteq \Args\) a subset of these arguments. The extensions are defined as follows:

• \(\SA\) is an admissible extension if and only if \(\SA\) is conflict-free, and all arguments \(A \in \SA\) are acceptable, with respect to \(\SA\).
• \(\SA\) is a complete extension if and only if \(\SA\) is admissible, and contains all acceptable arguments with respect to \(\SA\). In other words, \(\forall A \in \Args\), if \(\SA\) defends \(A\), then we must have \(A \in \SA\).
• \(\SA\) is a grounded extension if and only if \(\SA\) is a minimal complete extension, with respect to \(\subsetneq\), i.e., \(\not\exists \SA' \subseteq \Args\) such that \(\SA' \subsetneq \SA\) and \(\SA'\) is a complete extension.

Although there is no clear consensus in the community as to which extension should be used, the uniqueness property of some extensions, such as the grounded or ideal, makes them an attractive choice (Caminada, 2007). Indeed, this property means that we can compute the extension, and be guaranteed of its unicity, without worrying about having to implement in the judging agent a choice mechanism between possible sets. The grounded extension also has the advantage of being computed through a very efficient algorithm in \(\mathcal{O}\left(\length{\Args} + \length{\Att} \right)\) time, where \(\length{\Args}\) is the number of arguments in the whole graph, and \(\length{\Att}\) is the number of attacks between arguments in \(\Args\) (Nofal, Atkinson, & Dunne, 2021). For these two reasons, we will consider the grounded extension in our proposed model.

5.3.3 The proposed model: AJAR

We now present the Argumentation-based Judging Agents for ethical Reinforcement learning (AJAR) framework. In this proposed model, similarly to the logic-based model, we introduce judging agents to compute the rewards. Each judging agent has a specific moral value, and embeds an AFJD relative to this moral value.

Definition 5.5 (Argumentation-based Judging Framework) We define an Argumentation-based Judging Framework as a tuple \(\left\langle \JAgts, \left\{ AF_j \right\}, \left\{ \epsilon_j \right\}, \left\{ \Jj \right\}, \gagr \right\rangle\), where:

• \(\JAgts\) is the set of judging agents.
• \(\forall j \in \JAgts \quad \epsilon_j : \LAgts \times AF \times \StateSpace \to \mathcal{P}(AF_j)\) is a function that filters the AFJD to return the sub-AFJD that judging agent \(j\) uses to judge the learning agent \(i\).
• \(\forall j \in \JAgts \quad \Jj : \mathcal{P}(AF_j) \to \RR\) is the judgment function, which returns the reward from the sub-AFJD.
• \(\gagr : \RR^{\length{\JAgts}} \to \RR\) is the aggregation function for rewards.

To simplify, we consider that the \(\epsilon_j\) is the same function for each judging agent \(j\); however, we denote it \(\epsilon_j\) to emphasize that this function takes the AFJD associated to \(j\) as input, i.e., \(AF_j\), and returns a sub-AFJD \(\in \mathcal{P}(AF_j)\). The same reasoning is applied to the judgment function \(\Jj\).

The \(\epsilon_j\) function is used to filter the AFJD a judging agent relies on, according to the current state of the world. We recall that each argument of the AFJD has an alive condition function, which determines whether the argument is alive or not in this state. This means that designers create an AFJD with all possible arguments, and only the relevant arguments are retained during the judgment, through the \(\epsilon\) function.

Example 5.6 For example, an AFJD may contain 3 arguments: “the agent consumed 10% more than the average”, “the agent consumed 20% more than the average”, and “the agent consumed 30% more than the average”. At a given time step \(t\), in state \(s_t\), if the agent consumed 27% more than the average, the alive condition of the first two arguments will be true, whereas the last argument will be considered dead. Thus, when performing the judgment, the judging agent will only consider the first two, even for computing the grounded extension. Thanks to \(\epsilon_j\), the judgment acts as if the third argument was simply not part of the graph, and all its attacks are removed as well.

In the current definition, the \(\epsilon_j\) function assumes that judging agents have full knowledge about the world’s state \(s\). This allows comparing the learning agent to other agents, e.g., for the average consumption, which we cannot access if we only have the learning agent’s observations \(\mathbf{o_l}\). This assumption can be lifted by changing the definition of \(\epsilon_j\) to take \(\ObsSpace_l\) as domain; however, this would limit the available arguments, and thus the judgment as a whole.

The world’s state \(s\) consists of data from the true environment’s state and the agents’ actions. This represents some sort of very limited history, with the world state containing both the action itself and its consequences. A better history could also be used, by remembering and logging the actions taken by each agent: this would expand what the designers can judge within the argumentation graphs, e.g., behaviours over several time steps, such as first buying energy at \(t\) and then giving at \(t'\), with \(t' > t\). Note that actions from all learning agents are included in the world’s state, so that the currently judged agent can be compared to the others. This allows arguments such as “the learning agent consumed over 20% more than the average”.

For the sake of simplicity, we pre-compute a few elements from these continuous data, such as the average comfort, the difference between the maximum and minimum comfort, the quantity of energy the currently judged learning agent consumed, etc. These elements are made available to the judging agents so that they can filter the graph through \(\epsilon_j\). This pre-computation makes the argumentation graphs easier to design, as arguments, and by extension graphs and judging agents, can directly rely on these elements rather than performing the computation themselves, and it avoids some overhead when 2 different graphs use the same element.

From the filtered sub-AFJD, which only contains the alive arguments according to the current situation, we then compute the grounded extension to keep only the acceptable arguments, i.e., we remove arguments that are attacked and not defended. This produces an even more filtered graph \(\grd\), which only contains arguments that are both alive and in the grounded extension.

From this graph \(\grd\), we want to produce a reward as a scalar number: this is the goal of the judgment function \(\Jj\). There are multiple methods to do so, and we provide and compare a few in our experiments. Still, we give here an intuitive description to roughly understand what \(\Jj\) is doing. We recall that, in an AFJD, an argument may belong to the pros set, \(\Fp\), or the cons set, \(\Fc\). An argument that is in the pros set supports the decision that the agent’s behaviour was moral with respect to the moral value. \(\Jj\) intuitively counts the number of arguments in \(\FpInGrd\), and the number of arguments in \(\FcInGrd\) and compares them. The more pros arguments, the more the reward will tend towards \(1\); conversely, the more cons arguments, the more the reward will tend towards \(0\).

The \(\Jj\) function should however provide as much “gradient” as possible, i.e., an important graduation between \(1\) and \(0\), so that: 1) we can differentiate between various situations, and 2) we offer the agent an informative signal on its behaviour. If there is not enough gradient, we may have a case where the agent’s behaviour improves, in the human’s eye, but the reward does not increase, because the difference is too marginal. The agent would thus probably try another behaviour, to improve its reward, whereas its behaviour was already improving. On the contrary, if there is enough gradient, the reward will effectively increase, and this will signal the learning algorithm that it should continue in this direction. For example, if we suppose the number of cons arguments stayed the same, but the number of pros arguments increased, the resulting reward should increase as well, to indicate that the behaviour improved.

The described AJAR judging process is formally presented in Algorithm 5.6 and graphically summarized in Figure 5.7. The figure shows the process for a single learning agent, which is then repeated for each learning agent, as the formal algorithm shows with the for loop on the set of learning agents \(\LAgts\).

Figure 5.6: Argumentation-based judgment process algorithm

Figure 5.7: The judgment process of the AJAR framework, which leverages argumentation graphs to determine appropriate rewards. The argumentation graphs are first filtered based on the situation and the taken action to remove arguments that do not apply. Then, the reward is determined by comparing remaining pros and cons arguments.

Similarly to the previous algorithm, the for loop beginning on line 3 performs the judgment individually and sequentially for each learning agent. We compute the world state from all observations of all learning agents (line 5): this world state may contain some pre-computed values to simplify the arguments’ activation functions, such as “the learning agent consumed 27% more than the average”. Judging agents use this world state to filter out arguments that are not enabled, through the \(\epsilon_j\) function (line 7). This function returns the sub-AFJD that consists of all arguments whose activation function returns true for the current world state \(s\); attacks of disabled arguments are also removed. In Figure 5.7, these disabled arguments are in a lighter shade of grey. From this sub-AFJD, judges compute the grounded extension (line 8), by removing arguments that are killed and not defended by other arguments. To do so, we used the (efficient) algorithm proposed by Nofal et al. (2021). The per-judge reward is computed by comparing the pros and cons arguments remaining in the grounded extension (line 9); we describe a few methods to do so in Section 5.4.2. Finally, the per-judge rewards are aggregated into a scalar one for each learning agent (line 10); again, we compare several approaches in Section 5.4.2.

Remark (Value-based Argumentation Frameworks). Usually, AI systems that leverage argumentation and deal with (moral) values focus on Value-based Argumentation Frameworks (VAF) (Bench-Capon, 2002). In these frameworks, compared to our AFJD, each argument is associated to a value, and the framework additionally contains a preference relation over the possible values. This allows comparing arguments w.r.t. their respective values, such that an argument can be deemed stronger than another because its associated value is preferred. When using such frameworks, all arguments belong to the same graph and can thus interact with each other. On the contrary, in our approach, we proposed that different values are represented by different graphs, separated from each other. This means that an argument, relative to a given value, e.g., ecology, cannot attack an argument relative to another value, e.g., well-being. An advantage of this design choice is that we may add (resp. remove) moral values, i.e., argumentation graphs, without having to consider all possible interactions between the existing arguments and the new (resp. old) arguments. Yet, VAFs are well suited for decision-making, as they require the designer to consider such interactions when building the graph; we argue that using our AFJD is on the other hand suited for judgment-making.

5.4 Experiments

We have designed several experiments to evaluate our contribution, both on the logic-based and the argumentation-based agents. These experiments rely on the moral values we previously described in Section 3.4.5: security of supply, inclusiveness, environmental sustainability, and affordability. As for the previous experiments, we particularly emphasize the adaptation capability: in some scenarii, we incrementally enable or disable the judging agents. We recall that each judging agent is specific to a given moral value: in turn, this means that we add or remove moral values from the environment at different time steps. It might seem curious to remove moral values; we use this scenario as proof that, in combination with the ability to add moral values, we can effectively learn to follow evolutions of the ethical consensus within the society. Indeed, removing a previous moral value and adding a new one ultimately amounts to replace and update an existing moral value.

Remark. Note that, as the goal of this contribution is to propose an alternative way of specifying the reward function, i.e., through symbolic judgment rather than mathematical functions, the reward functions in these experiments are different from those used in the first contribution’s experiments in Section 4.5. Thus, the hyperparameters are not optimized for these new reward functions: the agents could attain a sub-optimal behaviour. However, we have chosen to avoid searching for the new best hyperparameters, in order to save computing resources. We will also not compare the algorithms to baselines such as DDPG or MADDPG. Indeed, we present here a proof-of-concept work on the usability of symbolic judgments for reward functions, and not a “competitive” algorithm. The goal is not to evaluate whether the algorithm achieves the best score, but rather to evaluate whether: 1) the reward function can be learned by the algorithm, and 2) the reward function implies an interesting behaviour, that is, a behaviour aligned with the moral values explicitly encoded in the function. These objectives do not require, per se, to use the best hyperparameters: if learning agents manage to learn an interesting behaviour by using sub-optimal parameters, it means that our proof-of-concept symbolic judgments can be used.

In both logic-based (LAJIMA) and argumentation-based (AJAR) models, we implement judging agents that represent the moral values detailed in Section 3.4.5:

• Security of supply, which motivates agents to satisfy their comfort need.
• Affordability, which motivates agents not to pay too much.
• Inclusiveness, which focuses on the equity of comforts between agents.
• Environmental Sustainability, which discourages transactions with the national grid.

Specific logic rules are detailed in Appendix C and argumentation graphs in Appendix D.

We design several scenarii, which notably depend on the 2 following variables:

• The environment size, i.e., the number of learning agents.
• The consumption profile, i.e., annual or daily.

These variables are exactly the same as in the previous chapter. We recall that a small environment corresponds to \(20\) Households, \(5\) Offices, and \(1\) School, whereas a medium environment corresponds to \(80\) Households, \(20\) Offices, and \(1\) School. The annual profile contains a consumption need for every hour of every day in a year, which we use as a target for agents: they want to consume as much as their need indicates; the daily profile is averaged on a single day of the year, and therefore does not contain the seasonal variations.

Additional variables are added separately for logic-based and argumentation-based experiments. In the sequel, we first describe experiments for logic-based agents, and then for argumentation-based agents.

5.4.1 Learning with LAJIMA judging agents

Our experiments leverage the Ethicaa agents (Cointe et al., 2016), which use the JaCaMo platform (Boissier, Bordini, Hübner, Ricci, & Santi, 2013). JaCaMo is a platform for Multi-Agent Programming that combines the Jason language to implement agents with CArtAgo for specifying environments with which agents can interact, and Moise for the organization aspect. We will particularly focus on the agent aspect, i.e., the Jason language (Bordini, Hübner, & Wooldridge, 2007), which is derived from AgentSpeak(L), itself somewhat similar to Prolog. The CArtAgo environment, defined in the Java programming language, allows us to connect the simulation and learning algorithms to the judging agents, by representing them as an artifact, storing the received observations and actions, and thus making them available to the judging agents. In addition, the CArtAgo environment is also responsible for sending rewards back to the simulation after the judgment process occurred. Judges continuously observe the shared environment and detect when new data have been received: this triggers their judgment plan. They push their judgments, i.e., the rewards, to the shared environment; once all rewards have been pushed, by all judging agents and for all learning agents, the environment sends them to the learning algorithm.

However, as we mentioned, JaCaMo relies on the Java language and virtual machine; our learning algorithms and Smart Grid simulator are developed in Python, we thus needed a way to bridge the two different codes. To do so, we took inspiration from an existing work that tries to bridge the gap between BDI agents, especially in JaCaMo, and RL (Bosello & Ricci, 2020), by adding a web server on the simulator and learning side. The CArtAgo environment then communicates with the simulator and learning algorithms through regular web requests: to ask whether the simulation is finished, whether a new step is ready for judgment, to obtain the data for judgment, and for sending back the rewards.

We now describe the scenarii that we designed, and which principally depend upon the configuration of judging agents. Indeed, we want to evaluate the ability to adapt to changing environment dynamics, especially in the reward function. Agentifying this reward function offers a new, flexible way to provoke changes in the reward function, by modifying the set of judging agents, e.g., adding, or removing. We thus developed the judges so that they can be activated or disabled at a given time step, through their initial beliefs, which are specified in the JaCaMo configuration file. The following configurations were used:

• Default: all judging agents are activated for the whole experiment: the rewards aggregate all moral values.
• Mono-values: 4 different configurations, one for each moral value, in which only a single judging agent is enabled for the whole experiment. For example, in the affordability configuration, only the affordability agent actually judges the behaviours. These scenarii serve as baselines.
• Incremental: At the beginning, only affordability is activated and produces feedbacks. We then enable the other agents one-by-one: at \(t=2000\), we add environmental sustainability, then inclusiveness at \(t=4000\), and finally supply security at \(t=6000\). From \(t=6000\) and up, all judging agents are activated at the same time.
• Decremental: Conversely to the incremental scenario, at the beginning, all judging agents are enabled. We then disable them one-by-one: at \(t=2000\), environmental sustainability is removed, then inclusiveness at \(t=4000\), and finally supply security at \(t=6000\). Afterwards, only the affordability agent remains.

5.4.2 Learning with AJAR judging agents

Similarly to the previous experiments, we designed several scenarii that are based on the following variables:

• The judgment function \(\Jj\) used to transform a grounded extension, and more specifically its \(\Fp\) and \(\Fc\) sets of arguments, into a single number.
• The aggregation function \(\gagr\) used to transform the different rewards returned by the judging agents into a single reward.
• The configuration of judges, i.e., which judges are activated and when.

The environment size and consumption profile are also used, as in the previous chapter and in the logic-based experiments. The other variables are described below with their possible values.

5.4.2.1 The judgment function

We recall that the judgment function \(\Jj\) is the last step of the judging process, before the aggregation. It takes as input the computed grounded extension of the argumentation graph, i.e., the graph that contains only arguments that are both alive and acceptable. Some of these arguments are in favour of the decision “The learning agent’s action was moral with respect to the moral value” and are said to be pros (\(\Fp\)), whereas other counter this decision and are said to be cons (\(\Fc\)). The rest of the arguments are neutral. From this grounded extension \(\grd\) and the sets \(\Fp\), \(\Fc\), the \(\Jj\) function must output a reward, i.e., a single number, that corresponds to which degree the agent respected the moral value.

Contrary to the logic-based LAJIMA model, where the number of moral valuations is fixed, in the argumentation-based AJAR framework, the number of moral valuations can be any number, only restricted by the total number of arguments. Indeed, the moral valuations are given by the \(\Fp\) and the \(\Fc\), and any argument can be a pro or con argument. Thus, many methods can be imagined for this judgment function. We have designed the following functions, which basically rely at some point on counting the number of \(\Fp\) and \(\Fc\), and comparing them. However, they differ in the exact details, which impact the gradient offered by the function, i.e., the possible values. Some functions will, for example, only be able to return \(\frac{0}{3}, \frac{1}{3}, \frac{2}{3}, \frac{3}{3}\), which has a low gradient (only 4 different values).

simple

Function that simply compares the number of \(\Fp\) with the sum of \(\Fp\) and \(\Fc\) in \(\mathit{grd}\).

\[\texttt{J}_{simple} = \begin{cases} \frac{\length{\FpInGrd}}{\length{\FpInGrd} + \length{\FcInGrd}} & \text{if } \length{\FpInGrd} + \length{\FcInGrd} \neq 0 \\ \frac{1}{2} & \text{else} \end{cases}\]

This function is simple and intuitive to understand, however, it fails to take into account difference when there are no arguments in \(\Fp\) or in \(\Fc\). To illustrate this, let us assume that, at a given step \(t\), there were 3 arguments in \(\FpInGrd\), and 0 in \(\FcInGrd\). The result is thus \(\frac{3}{3} = 1\). This correctly represents the fact that, at \(t\), the action only had positive evaluations (for this specific moral value). Let us also assume that, at another step \(t'\), there were still 0 arguments in \(\FcInGrd\), but this time 4 arguments in \(\FpInGrd\). One would intuitively believe that the action at \(t'\) was better than the one at \(t\): it received more positive evaluations. However, this function returns in this case \(\frac{4}{4} = 1\), which is the same reward. There is virtually no difference between an action with 3 or 4 pros arguments, as long as there is 0 cons arguments. The exact same problem applies with 0 arguments in \(\Fp\), which would invariably return \(\frac{0}{x} = 0\).

diff

Function that compares first the number of \(\Fp\) in the grounded with the total number of \(\Fp\) in the unfiltered, original, argumentation graph, then does the same for the number of \(\Fc\), and finally compares the \(\Fp\) and the \(\Fc\).

\[\texttt{J}_{diff} = \frac{\length{\FpInGrd}}{\length{\FpTotal}} - \frac{\length{\FcInGrd}}{\length{\FcTotal}}\]

Thus, this function is able to take into account the existence of non-activated arguments, either pros or cons, when creating the reward. For example, if only 3 of the 4 possible \(\Fp\) arguments are activated, the function will not return \(1\). Intuitively, this can be thought as “You have done well… But you could have done better.” In this sense, this function seems better than the previous one. However, a problem arises if some arguments are too hard to activate, and therefore (almost) never present in the \(\grd\), or if 2 arguments cannot be activated at the same time. The agent will thus never get \(1\), or conversely \(0\) in the case of \(\Fc\), because the function relies on the assumption that all arguments can be activated at the same time.

ratio

Function that compares the sum of the number of \(\Fp\) and \(\Fc\) with the maximum known of activated \(\Fp\) and \(\Fc\) at the same time.

\[\begin{align*} \mathit{top} & = \length{\FpInGrd}^2 - \length{\FcInGrd}^2 \\ \mathit{down} & = \length{\FpInGrd} + \length{\FcInGrd} \\ \mathit{max\_count}_{t} & = \max( \mathit{max\_count}_{t-1}, \mathit{down} ) \\ \texttt{J}_{ratio} & = \frac{\mathit{top}}{\mathit{max\_count}_{t}} \end{align*}\]

This function thus avoids the pitfalls of the previous one, by only comparing with a number of activated arguments that is realistically attainable. However, it still suffers from some drawbacks. For example, we cannot compute a priori the maximum number of activated arguments; instead, we maintain and update a global counter. This means that the rewards’ semantics may change over the time steps: a \(\frac{1}{2}\) might be later judged as a \(\frac{1}{3}\), simply because we discovered a new maximum. Taking this reasoning further, we can imagine that maybe, in a given simulation, the maximum known number will be 2 for most of the time steps, and finally during the later steps we will discover that in fact the maximum could attain 4. Thus, all previous rewards would have deserved to be \(\frac{x}{4}\) instead of \(\frac{x}{2}\), but we did not know that beforehand.

grad

Function that takes into account the total possible number of \(\Fp\) and \(\Fc\) arguments.

\[\texttt{J}_{grad} = 0.5 + \length{\FpInGrd} \times \left( \frac{0.5}{\length{\FpTotal}} \right) - \length{\FcInGrd} \times \left( \frac{0.5}{\length{\FcTotal}} \right)\]

This function creates a gradient between \(0\) and \(1\), with as many graduations between \(0.5\) and \(1\) as there are possible pros arguments, and conversely as many graduations between \(0.5\) and \(0\) as there are possible cons arguments. Each activated pro argument advances one graduation towards \(1\), whereas each activated con argument advances one graduation towards \(0\), with a base start of \(0.5\). This function is similar to diff, except that it stays within the \([0,1]\) range.

offset

Function that avoids division by \(0\) by simply offsetting the number of activated arguments.

\[\texttt{J}_{offset} = \min \left( 1, \frac{1 + \length{\FpInGrd}}{1 + \length{\FcInGrd}} \right)\]

Since neither the numerator nor the denominator can be \(0\), adding one \(\Fc\) argument without changing the number of \(\Fp\) would effectively change the resulting reward. For example, assuming \(\length{\Fp} = 0\), and \(\length{\Fc} = 3\), the reward would be \(\frac{1}{4}\). Adding one \(\Fc\) argument would yield \(\frac{1}{5}\), thus effectively reducing the reward. However, to avoid having rewards superior to \(1\), the use of the \(\min\) function prevents the same effect on \(\Fp\): if \(\length{\Fc} = 0\), the reward will be \(1\) no matter how many \(\Fp\) are present.

5.4.2.2 The aggregation function

As for the logic-based judgment, we have several judges that each provides a reward for every learning agent. Yet, the current learning agents expect a single reward: we thus need to aggregate.

We retain the average aggregation that was proposed for the logic-based, as it is a quite simple, intuitive, and often used method. Another option is to use a min aggregation that is based on the Aristotle principle. The Aristotelian ethics recommends to choose the action for which the worst consequence is the least immoral (Ganascia, 2007b). Adapting this reasoning to our judgment for learning, we focus on the worst value so that the agent will learn to improve the worst consequence of its behaviour. The final reward is thus the minimum of the judges’ rewards. The reward signal thus always focuses on the least mastered of the moral values. For example, assuming the agent learned to perfectly exhibit the inclusiveness value and always receives a reward of \(1\) for this moral value, but has not yet learned the value of environmental sustainability, and receives a reward of \(0.2\) for this second moral value, the reward will be \(0.2\) so that the agent is forced to focus on the environmental sustainability to improve its reward. When the agent’s mastery of the environmental sustainability exceeds that of other values, its associated reward no longer is the minimum, and another reward is selected so that the agent focuses on the new lowest, and so on. Thus, it emphasizes the learning of all moral values, not strictly at the same time, but in a short interval. The agent should not be able to “leave aside” one of the moral values: if this value’s reward becomes the lowest, it will penalize the agent. Formally, this function is simply defined as:

\[ \mathtt{g_{min}}\left(\Feedback(l)\right) = \min \left( \left\{ \forall f_{l,j} \in \Feedback(l) \right\} \right) \tag{5.1} \]

where \(\Feedback(l)\) is the set of rewards for the learning agent \(l\), of size \(\length{\JAgts}\), and \(f_{l,j}\) is the specific reward for learning agent \(l\) determined by judging agent \(j\).

However, I noticed that in some cases this function could become “stuck”. For example, if one of the argumentation graph is ill-defined, and it is impossible to get a high reward for one of the moral values, e.g., more than \(0.2\). In this case, as long as all other moral values have an associated reward \(\gneqq 0.2\), they will not be the minimum, and thus not selected by the \(\mathtt{g}_{min}\) aggregation. The agent therefore cannot receive feedback on its behaviour with respect to the other moral values. It would be difficult to improve further these moral values without feedback: even if the agent tries an action that improves another moral value, the “stuck” one will remain at \(0.2\), and thus be selected again, and the final reward will be \(0.2\). The received signal would seem to (wrongly) indicate that this action did not improve anything. It would not be a problem in the case of a few steps, because the agent would have later steps to learn other moral values. However, in this example scenario, as one of the moral values is “stuck”, even later steps would rise the same issue.

To potentially solve this concern, I proposed to introduce stochasticity in the aggregation function: the function should, most of the time, return the lowest reward so as to benefit from advantages of the \(\mathtt{g_{min}}\) function, but, from time to time, return another reward, just in case we are stuck. This would allow agents to learn other moral values when they fail to improve a specific one, while still penalizing this “stuck” value and avoid skipping the learning of this value. To do so, we propose the Weighted Random function, in which each reward has a probability of being selected, which is inversely proportional to its value, relatively to all other rewards. For example, if a reward is \(0.1\), and the other rewards are \(0.8\) and \(0.9\), then the \(0.1\) will have an extremely high probability of being selected. Yet, the two others will have a non-zero probability. Formally, we define the function as follows:

\[ \mathtt{g_{\textsc{WR}}}\left(\Feedback(l)\right) = \text{draw } f_{l,X} \sim P(X = j) = \frac{1 - f_{l,j}}{\displaystyle\sum_{k \in \JAgts} \left(1 - f_{l,k}\right)} \tag{5.2} \]

where \(X\) is a random variable over the different judging agents, \(\JAgts\), and \(f_{l,X}\) is the reward determined by judging agent \(X\).

5.4.2.3 Configuration of judges

Finally, we propose, similarly to the logic-based judges, several configurations of argumentation judges. Judges can be enabled or disabled at a given time step, and we thus use it to evaluate the adaptation to changing reward functions. The 3 following configurations have been tested:

• Default: all judging agents are activated, all the time.
• Incremental: Only the affordability agent is enabled at the beginning, then the environmental sustainability agent is activated at \(t=2000\), followed by the inclusiveness agent at \(t=4000\), and finally the supply security agent at \(t=6000\). All agents are thus enabled after \(t=6000\).
• Decremental: Basically the opposite of incremental, all agents are initially activated. At \(t=2000\), the environmental sustainability agent is disabled, the inclusiveness agent is disabled at \(t=4000\), and finally the supply security agent at \(t=6000\). Only remains the affordability agent after \(t=6000\).

5.5 Results

We first present the results for the LAJIMA model, using logic-based agents, and then for the AJAR framework, using argumentation-based agents. As for the previous chapter, the score here is defined as the average global reward at the end of the simulation, where the global reward is the mean of rewards received individually by learning agents, at a given step.

5.5.1 Learning with LAJIMA judging agents

Figure 5.8 shows the results for the experiments on each scenario. Results show that, on most scenarii, Q-SOM and Q-DSOM algorithms perform similarly, except on the env_sustain mono-value configuration, i.e., when only the judge associated to the Environmental Sustainability value is activated.

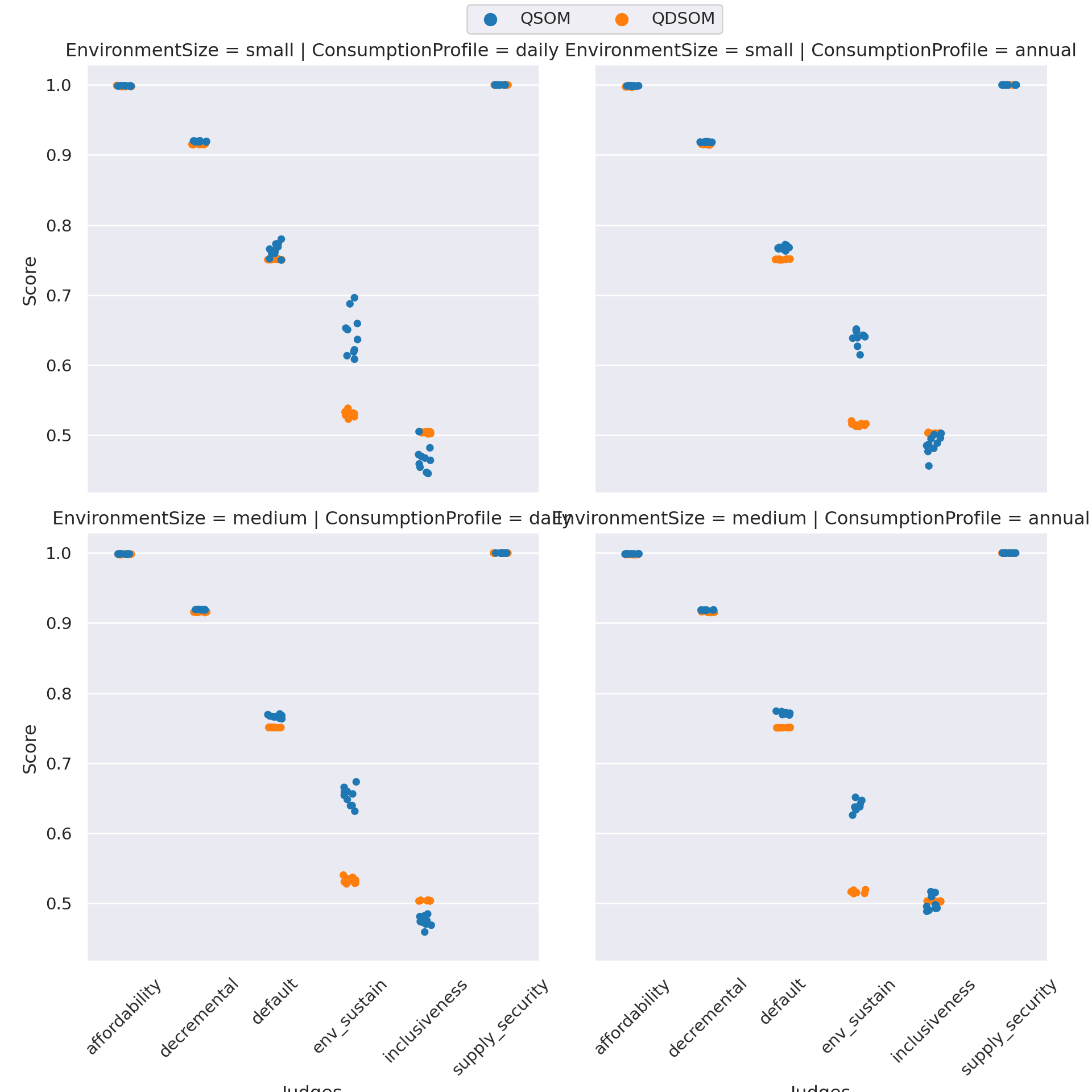
Figure 5.8: Results of the learning algorithms on 10 runs for each scenario, when using the LAJIMA agents.

Some moral values seem easier to learn, e.g., the affordability and supply_security scenarii, which consistently have a score of nearly \(1\). Others, such as the inclusiveness, seem harder to learn, but nevertheless attain a score of \(0.5\).

A statistical comparison between the small and medium sizes of environments, using the Wilcoxon test, does not show a significant difference in the obtained difference (p-value = 0.73751; we cannot accept the alternative hypothesis of a non-0 difference). This shows the scalability of our approach.

5.5.2 Learning with AJAR judging agents

Figure 5.9 shows the scores for the argumentation-based experiments. As we have detailed, in the AJAR framework, 2 additional parameters must be set: the judgment function \(\Jj\) that returns a single number from a set of moral evaluations, and the aggregation function \(\gagr\) that returns a final reward from the set of judgments for each judge. We can see that, for every choice of \(\Jj\) and \(\gagr\), and for every scenario, the learning algorithms managed to attain a very high score, superior to \(0.9\). This means that the judgment functions offer a good enough gradient to allow learning algorithms derive the correct behaviour from the reward signal.

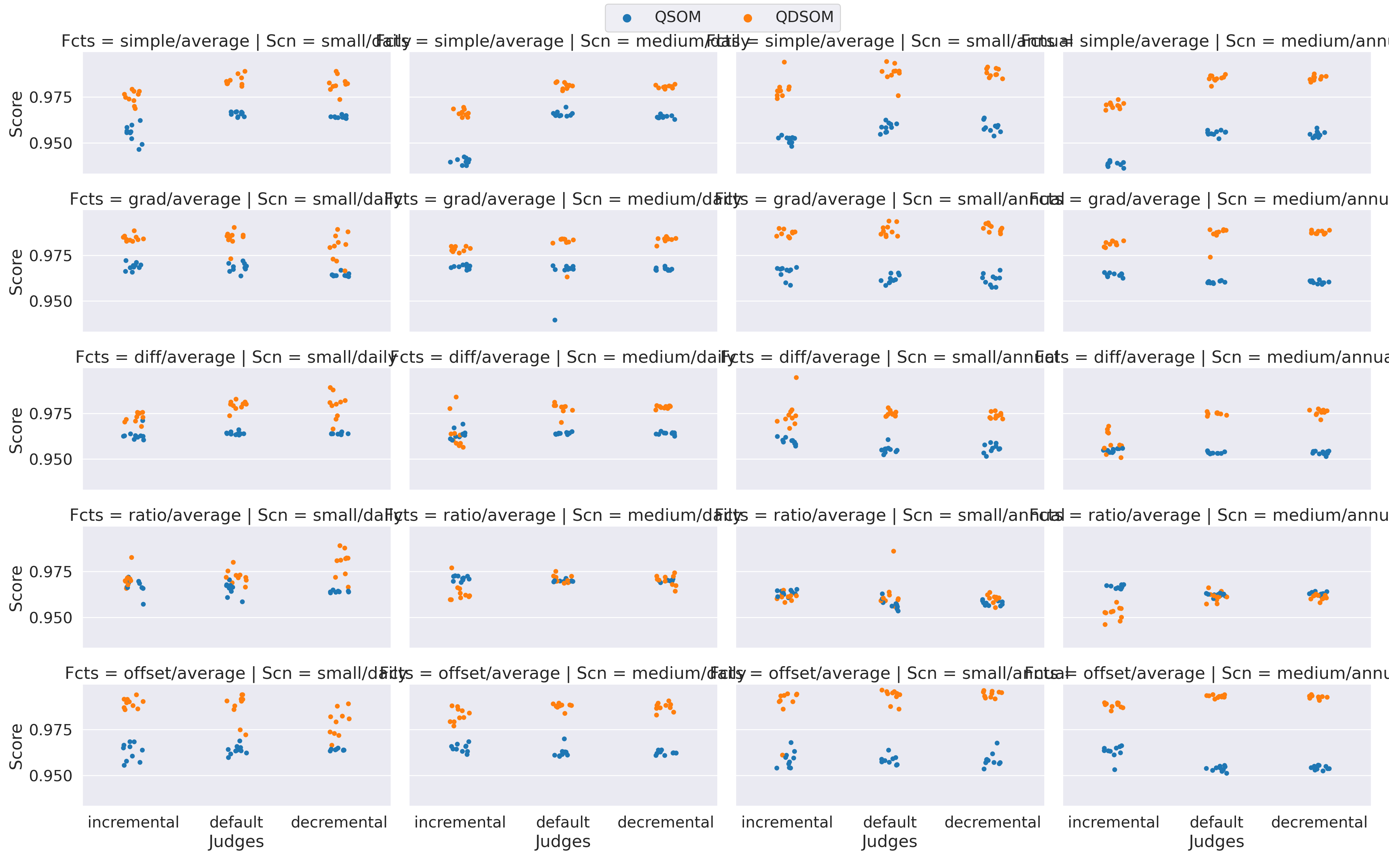
Figure 5.9: Results of the learning algorithms on 10 runs for each scenario, when using the argumentation-based judging agents. To simplify the plot, Scn (Scenario) regroups EnvironmentSize and ConsumptionProfile; Fcts (Functions) combines the choice of judgment and aggregation functions.

However, they are differences between different judgment functions. The offset, grad, and simple seem indeed to yield slightly higher rewards.

Interestingly, we can note that the Q-DSOM algorithm performs better on most of the experiments, compared to the Q-SOM algorithm. This is confirmed by a Wilcoxon test, using the “greater” alternative (p-value = < 2.22e-16).

5.6 Discussion

In this chapter, we presented a new line of research for constructing reward functions, through the use of symbolic judgment. More specifically, we proposed to introduce new judging agents to the multi-agent system, which judge the behaviour of the learning agents to compute their rewards, by leveraging symbolic reasoning, through either logic-based rules or argumentation frameworks. To the best of our knowledge, this line of research has not been studied, especially within Machine Ethics.

We recall that the principal objectives we identified from the state of the art were:

• How to correctly judge a learning agent’s behaviour, and particularly avoiding reward gaming?
• How to include a diversity of moral values?

By using symbolic judgments, we can leverage domain experts’ knowledge to correctly judge the learning agents. This is even more true with argumentation-based judgments, as the attack relationship can be leveraged to disable arguments in a specific context. We have given the fictional example of an agent that learned to hoard then give energy, to demonstrate how this kind of reward gaming could be fixed, by adding a new argument that checks whether the agent hoarded energy at the previous step. When this argument is true, the arguments that would tend to reward the agent for giving energy are disabled through the attacks. Using argumentation also helps with identifying a behaviour that exhibits reward gaming, by looking at arguments’ activation throughout the time steps.

Multiple moral values can be represented by different judging agents; using distinct agents instead of a single one offers several advantages. The agents can be individually added, updated, or removed, thus giving the designers control over the represented moral values in the system at runtime. Additionally, this paves the way to more complex interactions between the judging agents, which we will detail later.

The methods proposed in this chapter, logic-based and argumentation-based, have various specificities, and we now compare them, both to the traditional mathematical reward functions, and between them. We note that, as we have 2 different implementations, some differences, advantages or drawbacks, emerge from the technical implementation details, whereas others stems from more fundamental elements. The implementation differences are still important to note, even though they do not reflect a fundamental flaw or inherent advantage of the method; we will therefore particularly emphasize whether our remark is related to a technical implementation choice, or a fundamental conception, in the sequel. We also highlight the limitations and perspectives that arise from these methods.

First, we compare the two methods to the traditional mathematical functions, as used in the previous chapter. As we saw in the state of the art, multiple works have tried to implement ethical principles or moral values as symbolic rules. Such formalization seems therefore appropriate, when comparing to mathematical formulas, or more general programming languages. However, we note that one disadvantage of our chosen symbolic methods, when applied to the problem of generating rewards for learning agents, is to offer a poorer gradient than mathematical formulas, as we have already mentioned. By gradient, we mean that a difference in the situation and/or action should result in an equivalent difference in the reward, no matter how small the initial difference may be. The thinnest the gradient is, the more agents will learn when trying new behaviours: by exploring a new action, the result will be different, and this difference will be reflected in the reward, either positively or negatively. If the reward is better than before, the agent will then learn that this new action was a good one, and will retain it, rather than the old one. On the other hand, if the gradient is too coarse, the action difference induced by the learning agent risks not being correctly captured by the judgment. This is particularly visible when we think of thresholds for example: let us assume that we evaluate the action as moral if the agent did not consume more than 10% more energy than the average. At a first step \(t_0\), the agent may consume 20% more, and thus not being positively rewarded. At a second step \(t_1\), the agent may randomly consume 12% more than the average: the action is clearly better, however it is still above the threshold of 10%, and thus the agent is still not positively rewarded. It therefore has no feedback indicating that its action was better, yet not sufficient, but that it could continue in this direction. On contrary, mathematical functions offer a gradient by principle: let us take for example, \(R = consumed - (average \times 1.1)\), which represents roughly the same idea: the agent should not consume more than 110% of the average. We can clearly see that the reward will be different when the agent consumes 20% more, or 12%. It would even be different if the agent consumed 19.99999% more. This problem might be mitigated by other techniques, such as fuzzy logic (Zadeh, 1965), or weighted argumentation frameworks (Coste-Marquis et al., 2012), for example, which handle more naturally continuous values in addition to symbols.

This problem of gradient is linked with the notion of moral evaluation that we proposed in our methods. The symbolic rules produce these evaluations, which are in the form of \(\moral\) and \(\immoral\) symbols in the LAJIMA model, or represented by pros (\(\Fp\)) and cons (\(\Fc\)) arguments in AJAR. Then, the reward is determined based on these evaluations, the number of positive evaluations compared to the negative ones, etc. We note a first difference, which is purely an implementation detail, between our two methods: in LAJIMA, we have chosen to produce exactly as much evaluation as there are dimensions in an action; thus, each action dimension is judged and associated with a moral evaluation. On the contrary, in AJAR, we can have as many pros and cons arguments, and thus moral evaluations, as we desire. These 2 choices have both advantages and disadvantages: on the first hand, LAJIMA simplifies the problem by setting a fixed number of evaluations. Producing a reward can be as simple as dividing the number of \(\moral\) evaluations by the sum of \(\moral\) and \(\immoral\) evaluations. On the other hand, AJAR is more permissive, and offer more flexibility, in particular for the reward designers, who do not have to exactly set 6 evaluations, and may instead create the arguments as they see fit. It also opens the way for different methods to produce rewards: we proposed a few non-exhaustive options in our experiments to illustrate this. This may be seen as a disadvantage, since it requires an additional parameter for selecting the judgment function, which implies fine-tuning. Yet, this disadvantage seems justified, as the experiments tend to show a better gradient for the AJAR framework.

We note a first perspective here, about this judgment function; indeed, designing and selecting such a function to transform a set of symbols into a reward is not a trivial task. There is maybe more work to perform here, and we identify 2 potential (non-exhaustive) research avenues. First, the judgment aggregation theory domain may be leveraged, in order to correctly choose a number to represent a set of diverging evaluations. Secondly, an idea that is more specific to the AJAR framework, the argumentation graphs could be replaced by weighted ones. Indeed, we used a simple argumentation framework in our proof-of-concept work: the attack relationship is a simple, unidirectional one. If an argument is attacked, and not defended by another, it is considered killed. However, other argumentation frameworks exist in the literature, such as the weighted argumentation graphs (Coste-Marquis et al., 2012 ; Amgoud, Ben-Naim, Doder, & Vesic, 2017), where arguments and attacks are augmented by a notion of weight. An argument that has a significant weight will not be killed if it is attacked by an argument with a smaller weight. However, it might be killed if several arguments with small weights attack it, and so on. The idea here, to ultimately improve the judgment function, would thus be to rely on the remaining arguments’ weights to produce the reward. If an argument is attacked but not killed, its weight will be reduced, so that we can say the agent “did well, but not enough”: this avoids the pitfalls of thresholds mentioned earlier. To compute the final reward, the judgment function could, e.g., sum the weights of pros arguments and subtracts the weights of cons ones.

Another difference that comes from a technical implementation detail is the kind of inputs used by judging agents. Indeed, the logic-based ones in LAJIMA rely on the individual learning agents’ observations and actions: this is inspired by the Ethicaa work, which describes this as a partially informed judgment, i.e., a judgment where the judge uses knowledge from the judged agent, especially about the situation and the agent’s action. Intuitively, we can see this kind of judgment as “Would I have done the same thing, had I been at this agent’s place?”. On contrary, in AJAR, we described the input of the argumentation graphs as the whole knowledge of the current state, e.g., including data about other agents. This allows for example to compute the average consumption, and compare the judged agent’s consumption to the entire society. Since all data are included, the judging agents could also compare it to the median, or the 1st quartile, etc. This makes judging agents sort of “omniscient”, thus making more accurate judgments, but potentially impairing the privacy, since more data are shared. However, we note that the judging agents are meant as some sort of central controller, and are external to the learning agents. Thus, a Smart Grid participant still cannot access their neighbors’ data. There is most certainly an important question to ask and answer here, about the correct tradeoff between the accuracy of judgments, and the privacy of the human users. Some of them will probably not want to share data. We leave this question aside, as our work does not concern the acceptability of Smart Grid (or more generally, AI) systems, but we acknowledge that the ability to correctly judge, and ultimately learn, ethical behaviours may be limited by this acceptability concern.

One of the fundamental differences between our 2 proposed models is the kind of symbolic elements that are leveraged. In LAJIMA, logic rules are used, along with beliefs, and plans, whereas AJAR uses arguments and graphs. This has an impact on the ability to read and understand the reward function, i.e., the expected behaviour, by designers first, but more importantly by non-experts people. For example, the well-known Mycin (Buchanan & Shortliffe, 1984) example has shown that expert systems, which rely on similar rules to our LAJIMA model, were difficult to understand by doctors, although it could theoretically “explain” its reasoning by showing the trace of rules that were triggered. More importantly, it was difficult for users to integrate their own knowledge in the system. Arguments’ activation allows visualizing the reasoning as a graph and see the attacks as a map, which may be easier to understand for lay users rather than plans and beliefs. Graphs are updated by adding (or removing) arguments (nodes), and specifying the attacks on other arguments, visually represented by edges; this, again, may be easier to use rather than rules laid out in a textual format, for domain experts who are not versed in AI development. However, we did not test this hypothesis with a Human-Computer Interaction experiment, and more work is required on this subject.

Both our models have a small limitation linked to the simplification of their definition. Indeed, we consider a set of judging agents, with each judge representing a moral value, and we define a symbolic judgment with respect to this moral value. However, one might argue that moral values are not the only important objectives: there might be some others, that we denote “technical aims”, or aims for short, which are important for the system but not especially linked to a moral value. An example of such aims may be, for example, to correctly balance the production and consumption within a Smart Grid. If these aims can be computed as a symbolic judgment, they can be added to the system exactly as the moral values are, without loss of generality. However, some aims may be easier to design as a mathematical function, as the example above, which can be simply formulated as a difference between the production and the consumption. The current model does not allow this. The formal definitions of the model can be extended to consider not only the set of judging agents, but rather the union of judges with aims functions. Thus, the aggregation function takes the symbolic-produced rewards for moral values and the rewards for aims. Considering this union is not difficult from a technical point of view, but complicates the definition and diverts attention from the important part of the contribution, we thus chose to leave it aside.

Finally, another important element is the choice of the aggregation function. Indeed, the learning algorithms, in their current form, require a single reward per learning agent, whereas we have multiple judging agents representing various moral values. We thus need to aggregate, and we proposed several methods to do so: the average function, which is probably the most classical and intuitive way, the min function, which is almost as classical, and finally our custom Weighted Random, which mimics the behaviour of min while adding stochasticity to avoid “stuck” situations. Perhaps other functions could be explored, e.g., in computational social choice (Chevaleyre, Endriss, Lang, & Maudet, 2007), and more specifically in multi-criteria decisions, several approaches have been proposed to replace min-based aggregation, such as ordered weighted min, or leximin (Dubois, Fargier, & Prade, 1997). Basically, the idea of these approaches is to introduce some kind of preference or priority over the various criteria. They have been thoroughly explored within the field of social choice, especially for fair division, for decision-making purposes. However, in our case, the “decision” is not to select an action, e.g., a way to distribute resources among agents, but rather to select a reward that will be used to learn the correct action. This (subtle) difference calls for more research and experiments to apply such approaches to the problem of reward selection, in order to avoid pitfalls. For example, who should set the preferences over moral values? Should it be the designers, using the same preferences for all agents, or the users, using their own (different) preferences for their own agent? In this second case, would users be able to make their agent “ignore” of the moral values by carefully crafting their preferences? Should we allow them this possibility? And how can we prevent them from doing so?

The choice of the aggregation function is important for the resulting behaviour, as it determines how the moral values are learned, in which order, how the system handles values of different “difficulties”, and situations where values are in conflict. Yet, the scalarization idea is not ideal: by principle, scalarizing makes us lose information. Whether we take an average, a min, or a random reward among those proposed, we still send less feedback to the agent than with the full set of rewards. We have identified 2 groups of ideas to replace it: 1) An improved interaction between judging agents, e.g., through negotiation. In a sense, the judgment aggregation theory mentioned earlier could belong to this group. Thus, the final reward is itself constructed by reasoning. If, for example, one of the judging agents detects that its moral value is not correctly learned, because the learning agent keeps repeating the same mistakes, it can negotiate with other judges to emphasize its reward, or on contrary to ignore it, in order to focus on other moral values and avoid preventing their learning. This can be achieved, e.g., by negotiation between the judging agents themselves, or by creating a meta-reasoning agent, which takes the results of the lower-level judges as inputs, and outputs the final reward. This meta-judge could therefore include ethical principles to decide, whereas the other judges would include rules that concern only their moral value. This idea could be extended to create rewards that do not only depend on the current judgments at step \(t\), but on the whole history of the learning agent. For example, the meta-judge could decide that, although the learning agent’s action was good at this step, it could have been better, and thus award only a small amount to the learning agent, to encourage it to improve. Or, on the contrary, the meta-judge could give a higher reward even though some moral value is not respected, to help the agent learn the other values first, in some sort of adversarial or active learning loop. 2) Instead of aggregating the judgments per moral value into a single reward for each learning agent, we could simply send all feedbacks to them. Thus, the learning agents get more information, and can identify situations where 2 moral values are in conflict. This new ability can be exploited to inject human users’ preferences inside the learning agents to resolve these conflict situations, in a way that is specific to each learning agent, and thus to each human user.

We note that, by aggregating the moral values, we settle potential dilemmas a priori. This prevents the learning agents from correctly handling these dilemmas, and even recognizing there was a dilemma in the first place. We will therefore, in the next chapter, explore this 2nd family of ideas, which leads to a multi-objective approach for the learning algorithm. Scalarizing was necessary as a first step, in order to evaluate the contribution of agentifying the reward function and leveraging symbolic judgments on its own. Then, we “open up the box”, by sending directly multiple rewards, one for each moral value, to each learning agent. This way, they can compare the rewards, recognize situations of dilemmas, and each learning agent can settle dilemmas in a different way, depending on both the context and their user’s preferences. For example, user A may favor the inclusiveness value, and thus the learning agent will choose actions that yield maximal rewards for this value when it cannot optimize all of them. Another user, B, may favor on contrary the affordability value, and thus its own learning agent will learn differently from user A’s agent. In a different context, e.g., in winter instead of summer, perhaps user A may also favor the affordability value, and the learning agents will have to learn this.

References

Alcaraz, B. (2021). Argumentation-based judging agents for ethical reinforcement learning supervision (Master’s thesis). Université Claude Bernard Lyon 1.

Amgoud, L., Ben-Naim, J., Doder, D., & Vesic, S. (2017). Acceptability semantics for weighted argumentation frameworks. In Twenty-sixth international joint conference on artificial intelligence.

Amgoud, L., Cayrol, C., Lagasquie-Schiex, M.-C., & Livet, P. (2008). On bipolarity in argumentation frameworks. International Journal of Intelligent Systems, 23(10), 1062–1093.

Amgoud, L., & Prade, H. (2009). Using arguments for making and explaining decisions. Artificial Intelligence, 173(3-4), 413–436.

Bench-Capon, T. (2002). Value based argumentation frameworks. arXiv Preprint Cs/0207059.

Boissier, O., Bordini, R. H., Hübner, J. F., Ricci, A., & Santi, A. (2013). Multi-agent oriented programming with JaCaMo. Science of Computer Programming, 78(6), 747–761.

Bordini, R. H., Hübner, J. F., & Wooldridge, M. (2007). Programming multi-agent systems in AgentSpeak using jason. John Wiley & Sons.

Bosello, M., & Ricci, A. (2020). From programming agents to educating agents – a jason-based framework for integrating learning in the development of cognitive agents. In L. A. Dennis, R. H. Bordini, & Y. Lespérance (Eds.), Engineering multi-agent systems (pp. 175–194). Cham: Springer International Publishing.

Buchanan, B. G., & Shortliffe, E. H. (1984). Rule based expert systems: The mycin experiments of the stanford heuristic programming project. Addison-Wesley Longman Publishing Co., Inc. Retrieved from https://www.shortliffe.net/Buchanan-Shortliffe-1984/MYCIN%20Book.htm

Caminada, M. (2007). Comparing two unique extension semantics for formal argumentation: Ideal and eager. In Proceedings of the 19th belgian-dutch conference on artificial intelligence (BNAIC 2007) (pp. 81–87). Utrecht University Press.

Chaput, R., Duval, J., Boissier, O., Guillermin, M., & Hassas, S. (2021). A multi-agent approach to combine reasoning and learning for an ethical behavior. In Proceedings of the 2021 AAAI/ACM conference on AI, ethics, and society (pp. 13–23).

Chevaleyre, Y., Endriss, U., Lang, J., & Maudet, N. (2007). A short introduction to computational social choice. In International conference on current trends in theory and practice of computer science (pp. 51–69). Springer.

Cointe, N., Bonnet, G., & Boissier, O. (2016). Ethical judgment of agents’ behaviors in multi-agent systems. In Proceedings of the 2016 international conference on autonomous agents & multiagent systems (pp. 1106–1114). Richland, SC: International Foundation for Autonomous Agents; Multiagent Systems.

Coste-Marquis, S., Konieczny, S., Marquis, P., & Ouali, M. A. (2012). Weighted attacks in argumentation frameworks. In Thirteenth international conference on the principles of knowledge representation and reasoning.

Dubois, D., Fargier, H., & Prade, H. (1997). Beyond min aggregation in multicriteria decision:(ordered) weighted min, discri-min, leximin. In The ordered weighted averaging operators (pp. 181–192). Springer.

Dung, P. M. (1995). On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artificial Intelligence, 77(2), 321–357.

Duval, J. (2020). Judgment of ethics of behavior for learning (Master’s thesis). Université Claude Bernard Lyon 1.

Ganascia, J.-G. (2007b). Modelling ethical rules of lying with answer set programming. Ethics and Information Technology, 9(1), 39–47.

Li, H., Oren, N., & Norman, T. J. (2011). Probabilistic argumentation frameworks. In International workshop on theorie and applications of formal argumentation (pp. 1–16). Springer.

Nofal, S., Atkinson, K., & Dunne, P. E. (2021). Computing grounded extensions of abstract argumentation frameworks. The Computer Journal, 64(1), 54–63.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353.